Standing Wave

Sound and Resonance > Standing Wave

Standing wave (Transverse wave)

Two sine waves with the same Amplitude, Wavelength and Frequency travelling in opposite directions will interfere and produce a combined wave (Figure 1). The waveform of the combined waves, on average has No Net Propagation of Energy and is known as standing wave.

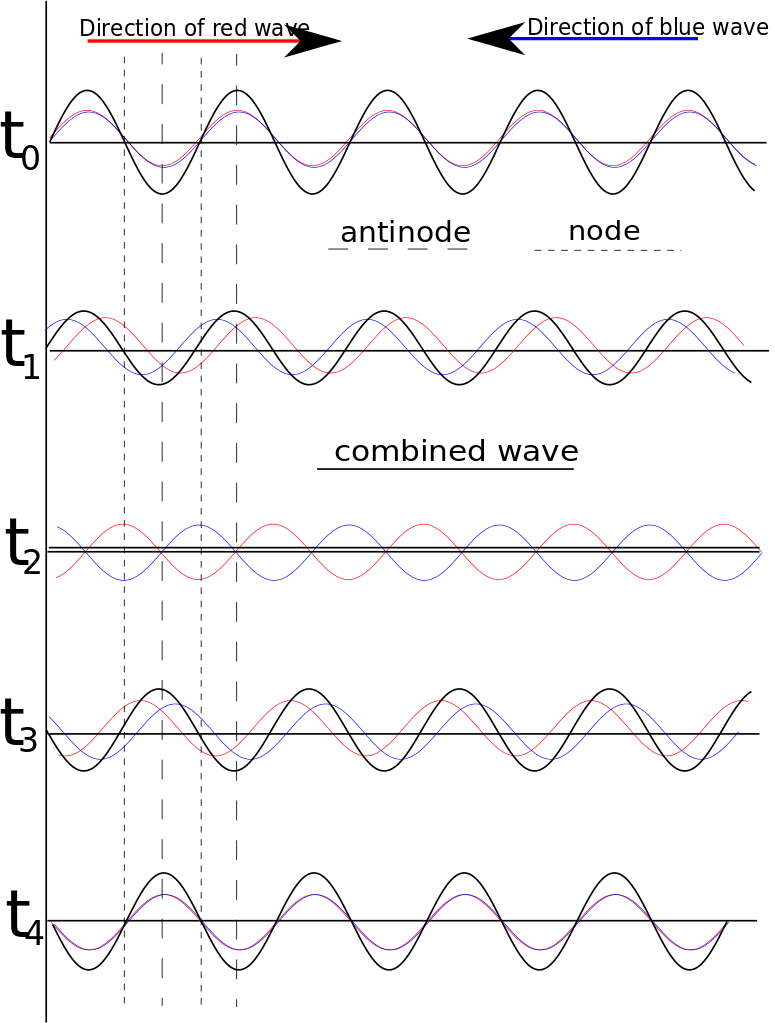
Figure 1: Formation of Standing Wave

Property of standing wave:

(1) Nodes: Points which are stationary and with zero amplitude. At nodes, two waves travel in exactly same amplitude and out of phrase offset with each other. (Figure 2).

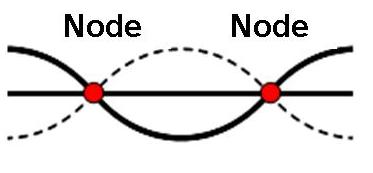
Figure 2: Nodes of Standing Wave

(2) Antinodes: Points at maximum amplitude. At antinodes, two waves travel in exactly same amplitude and in phrase reinforce with each other. (Figure 3).

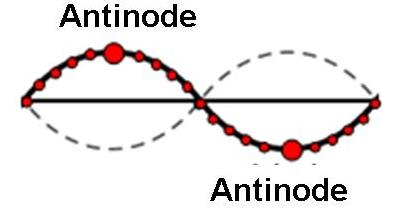
Figure 3: Antinodes of Standing Wave

(3) The maximum amplitude of each particle is related with its position and each amplitude oscillates periodically.. (Figure 4).

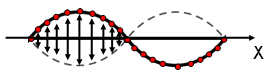
Figure 4: Amplitude at different particles of the Standing Wave

(4) The distance between two adjacent nodes or two adjacent antinodes is equal to half of the wavelength (Figure 5).

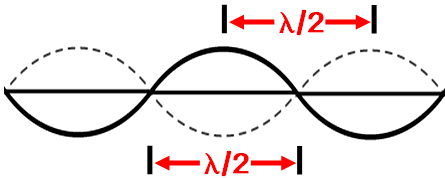
Figure 5: Distance between nodes or antinodes

(5) As the displacement of the nodes is always zero, the waveform is not travelling. Hence energy is confined between two adjacent nodes.

Standing wave of two fixed ends:

In Figure 6, the length of the string is L. The two fixed ends are nodes. In between them, there can be with or without nodes. The positions of the nodes and antinodes are shown in the figure. The length of the string is multiples of half of the wavelength.

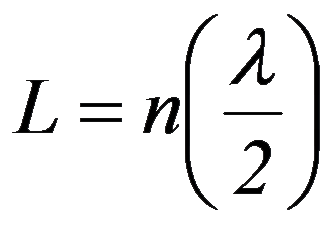
or

Since the velocity of the wave is

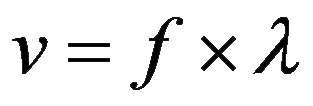
, where f is frequency, therefore:

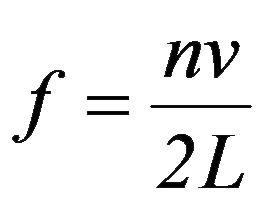
(n is a positive integer)

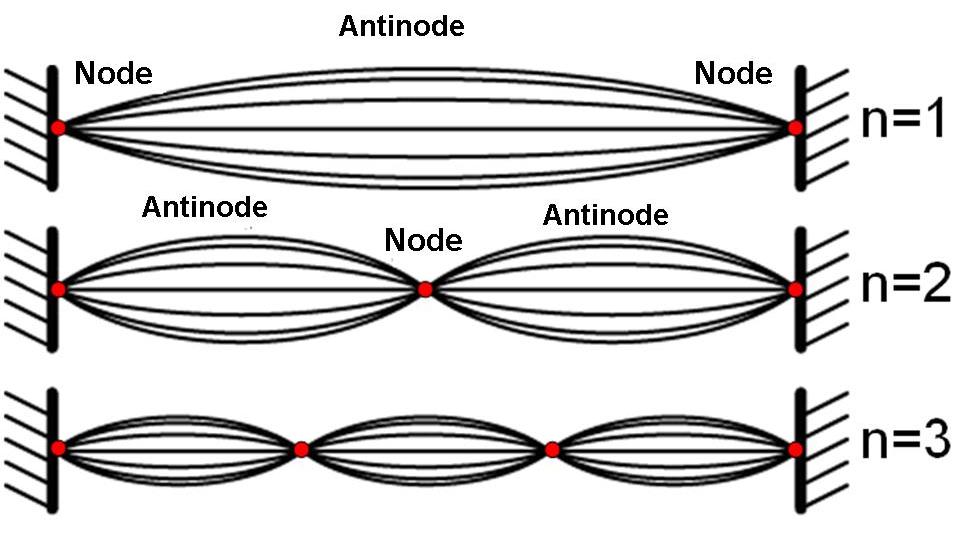
Figure 6: Standing wave of two fixed ends

Two-dimensional Standing Wave Patterns – Chladni Patterns

The standing wave patterns formed on Two-dimensional flat plates, are called Chladni Patterns (Figure 7)

Figure 7: Chladni Patterns

Formation of Chladni Patterns:

Lay a thin layer of sand on a flat horizontal plate and produce standing waves on the plate by making vibration. Nodes and antinodes will be formed on different parts of the plate. The sand on the antinodes will jump to other positions, whereas the sand on the nodes will remain stationary. After a while, certain amount of sand will be accumulated on the nodes and form nodal lines (Figure 8). The patterns will change according to the frequency of vibration but general speaking, they are symmetrical patterns.

Figure 8: Structure of Chladni Patterns

Links

Sound and Resonance > Standing Wave