Total internal reflection
As shown in Figure 1, when a Light Beam hits the Boundary between two different Media, Medium 1 and Medium 2, with a certain Angle of Incidence, i, part of it is Refracted at an Angle of Refraction, r, and other part of it is Reflected back to its original Medium at an Angle of Reflection, i', equal to the Angle of Incidence,i.
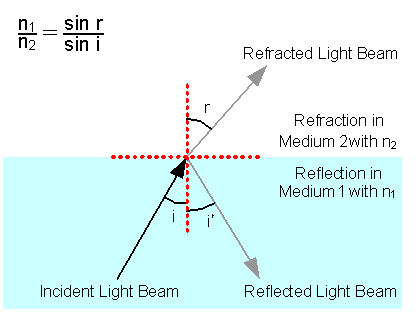 Figure 1: Refraction and Reflection of a Light Beam at the Boundary of two different Media
Figure 1: Refraction and Reflection of a Light Beam at the Boundary of two different Media
The Refractive Index, n, of a Medium is the ratio of the Speed of Light in Vacuum, c, to the Speed of Light through that Medium, v. That is, n = c/v. The Higher the Index, the Slower the Speed of Light through the Medium.
When a Light Beam travels from a Medium with Higher Refractive Index, n1, to a Medium with a Lower Refractive Index, n2, there is no Refraction if the Angle of Incidence is greater than a certain angle called the Critical Angle, θ, Figure 2. All the Light Beam will be Reflected back to the original Medium, this is called Total Internal Reflection.
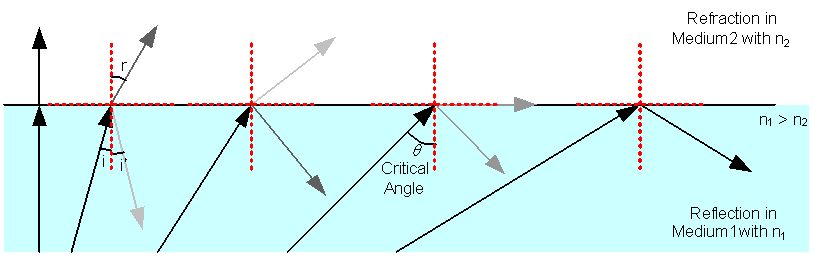 Figure 2: Refraction and Reflection of a Light Beam at the Boundary of two different Media at different Angles of Incidence
Figure 2: Refraction and Reflection of a Light Beam at the Boundary of two different Media at different Angles of Incidence
Given n1 and n2 as the Refractive Indices of Medium 1 and Medium 2, the Critical Angle θ of the Light Beam going from Medium 1 towards Medium 2 can be determine by the following formula:
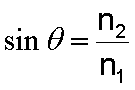
The Laser Beam stays inside of the Optical Fibers due to the Total Internal Reflection.
The Laser Beam degrades when propagates within the Medium, mostly due to the Impurities inside it. In real Optical Fibers, very pure Glass is used.
If the Glass has very little Impurities and a proper Frequency is used, the Laser Beam can propagate over distance of several kilometers with very little Attenuation.
About CMM
Contact US
Others
Other Websites
Number of Visitors:
Last Modified Date: 10/3/2025