逻辑门展区II

逻辑门是数码电子学中的基本组成部份。逻辑门输入和输出之间的关系可以用真值表来表示。

异或门是一种具有两个或多个输入的逻辑门，当输入中只有一个为1时，逻辑门的输出才为1。图1是一个二输入异或门的电路符号，而表1是它的真值表。

异或门所执行的逻辑运算可表示为：

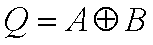
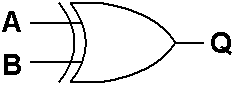
图1: 异或门的电路符号

A B Q

0 0 0

0 1 1

1 0 1

1 1 0

表1: 异或门的真值表

异或非门是一种具有两个或多个输入的逻辑门，只有当所有输入都为同一逻辑状态时，逻辑门的输出才为1。图2是一个二输入异或非门的电路符号，而表2是它的真值表。

异或非门所执行的逻辑运算可表示为：

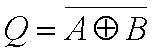
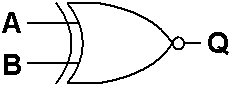
图2: 异或非门的电路符号

A B Q

0 0 1

0 1 0

1 0 0

1 1 1

表2: 异或非门的真值表

在电子学中，加法器是一种实现两个数加法运算的设备。

半加器是一种实现1位元加法的逻辑电路。P和Q都是1位元二进制数。S是P和Q的1位元和而CO是进位输出位元。图3显示数学上P和Q的2位元算术和，它由两个输出S和CO组成，其中CO是最高有效位元 (MSB)。图4是1位元加法的所有可能情况，表3是半加器的真值表。

1 ←P

+) 1 ←Q

1 0

↑ ↑

进位和

图3: 两个1位元二进数的加法运算

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 进位为1

图4: 1位元加法的所有可能情况

输入输出

P Q CO S

0 0 0 0

0 1 0 1

1 0 0 1

1 1 1 0

表3: 半加器的真值表

根据真值表的结果，若从逻辑运算上考虑半加器的输入输出关系，S是两个输入经过异或 (XOR) 运算的结果，而CO是两个输入经过与 (AND) 运算的结果。这表示半加器电路能够只用两种门电路实现：一个异或门和一个与门，见图5。

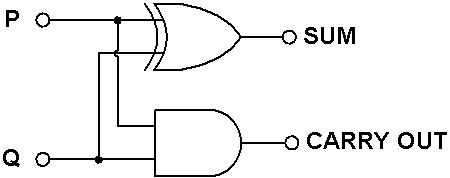
图5: 半加器

由于半加器不能接受来自低位相加所产生的进位位元作为输入，因此它只能执行两个1位元二进制数的加法。

基本 (1位元) 全加器是实现两个一位元二进数和一个进位输入CARRY IN (CI) 加法运算的逻辑电路。它由一个或门和两个半加器组成，见图6。整个电路产生两个输出：S 和CO。多个全加器可以串接起来形成一个多位元加法器。

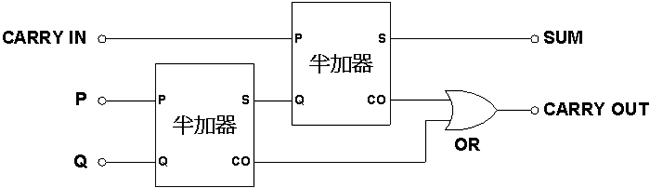
图6: 基本 (1位元) 全加器

若干个基本 (1位元) 全加器可以串级成多位元全加器。如图7所示，四个基本全加器被串级成一个4位元串行加法器，其中每个基本全加器的进位输出CO接到下一有效位的全加器的进位输入CI。

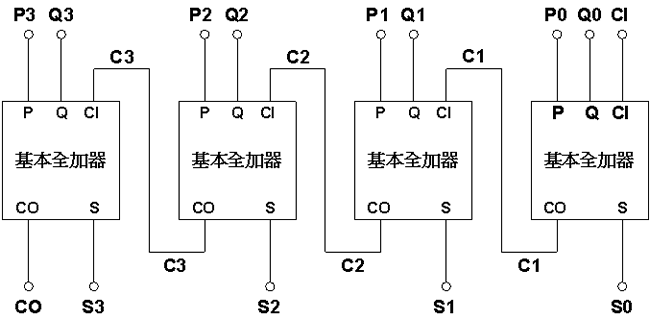
图7: 由四个基本全加器构成的4位元串行加法器

两个多位元二进制数P和Q的加法能够由它们的最低有效位元 (LSB) 的相加开始，即P0 + Q0。任何前一位元的进位会相加到紧接的下一位元的和，见图8。

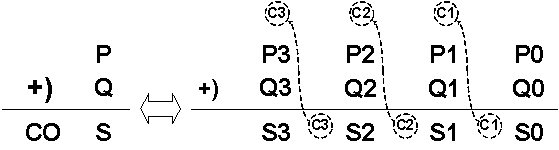
图8: 两个4位元二进制数加法进位运算说明

对于一个5位元二进制数P，它的各个有效位元的数权值是：

P0 = 2⁰ = 1

P1 = 2¹ = 2

P2 = 2² = 4

P3 = 2³ = 8

P4 = 2⁴ = 16

把一个5位元二进制数P2 (P4 P3 P2 P1 P0) 转换为相应的十进制数P₁₀的公式是:

P₁₀ = P4 x 2⁴ + P3 x 2³ + P2 x 2² + P1 x 2¹ + P0 x 2⁰

一个4位元全加器的进位位元CO等同输出的第4有效位元，而它的数权值为16 (2⁴ = 16)。

由一个4位元全加器可得到的最大十进制和是31 (2⁴⁺¹ ― 1 = 31)。